3.2.1结构重要性系数r0应按结构构件的安全等级、设计工作寿命并考虑工程经验确定。对设计工作寿命为25年的结构构件,大体上属于替换性构件,其可常度可适当降低,重要性系数可按经验取为0.95。
在现行国家标准《建筑结构荷载规范》)GB50009中、将屋面均布活荷载标准值规定为0.5kN/m2,并注明“对不同结构可按有关设计范将标准值作0.2kN/m2的增减”。本规范参考美国荷载超范ASCE7-95的规定,对支承轻屋面的构件或结构,当受荷的水平投面积超过60m2时,屋面均布活荷载标准值取为0.3kN/m2。这个取值仅适用于只有一个可变荷载的情况,当有两个及以上可交荷载考虑荷载组合值系数参与组合时(如尚有灰荷载),屋面活荷载仍应取0.5kN/m2,否则,将比原规范降低安全度(因为原荷载规范规定无风组合时不考虑荷载组合值系数)。
3.2.2本条对原规范中关于吊车横向水平荷载的增大系数α进行了修改(详见“重级工作制吊车横向水平力计算的建议”赵熙元,《钢结构》192年第2期)。该系数源出于前苏联《治金工厂重级工作制厂房钢结构设计技术条件》TY-104-53。但在1972年及以后的前苏联钢结构设计规范中已不再使用α系数,而在建筑法规《荷载及其作用》中,对重级工作制吊车的侧向力,不论计算吊车梁或连接均统一规定为TH≈0.1PH(PH为吊车最大轮压的标准值),并认为TH的作用方向是可逆的,且不与小车的制动力同时考虑。这种将吊车的横向水平力(俗称卡轨力,下同)与吊车轮压成正比的表达方式和德国的研究成果是一致的,理论上亦比较合理,日本1998年规范也是这样考虑的。因为卡轨力与吊车主动轮的牵引力成正比,而牵引力又与轮压成正比。原规范的表达方式似乎卡轨力仅与小车制动力有关,这在概念上是有问题的,因为制动力是由小车制动而产生,卡轨力则在大车运行时发生,两者的起因截然不同。另外,对没有小车的特殊吊车(如桥式螺旋式卸车机),按原规范就算不出卡轨力,显然很不合理。
要精确计算卡轨力是十分困难的,世界各国所采用的计算方法都是半经验半理论性的。目前,欧、美及日本各国在计算卡轨力时都不区分构件和连接。这次修订时,亦采用统一的卡轨力值。
本条在计算卡轨力时采用了Hk=αPk,max的表达式,其中α系数的取值是针对我国有代表性的9种重级工作制吊车,采用不同的计算方法(包括我国原规范、前苏联和美国的方法)算出的卡轨力,经过对比分析而得出来的。用本规范的公式(3.2.2)算出的卡轨力除A8级吊车是接近于按原规范计算构件的力以外,其余吊车均接近于按原规范计算连接时的力,而与美国的计算结果相近。亦即A6和A7级吊车按本规范算得的卡轨力约为原规范计算构件时卡轨力的2倍。从调查研究可知,过去设计的吊车梁在上翼缘附近的损伤仍然较多,因此加大卡轨力看来是合适的。根据试设计的结果,由此而带来的吊车梁钢材消耗量的增值一般约为5%。
本条的“注”中,提出了在一般情况下本规范所指的重级、中级及轻级工作制吊车的含义。《起重机设计规范》GB/T3811规定吊车工作级别为A1~A8级,它是按利用等级(设计寿命期内总的工作循环次数)和载荷谱系数综合划分的。为便于计算,本规范所指的工作制与现行国家标准《建筑结构荷载规范》GB50009中的载荷状态相同,即轻级工作制(轻级载荷状态)吊车相当于A1~A3级,中级工作制相当于A4、A5级,重级工作制相当于A6~A8级,其中A8为特重级。这样区分在一般情况下是可以的,但并没有全面反映工作制的含义,因为吊车工作制与其利用等级关系很大。故设计人员在按工艺专业提供的吊车级别来确定吊车的工作制时尚应根据吊车的具体操作情况及实践经验来考虑,不要死套吊车是检修吊车,过去一直按轻级工作制设计,按载荷状态很可用A4级吊车,便属于中级工作制。若按中级工作制吊车来设计厂房结构,显然不合理,此时可仍将其定义为轻级工作制。
3.2.3本条规定的屋盖结构悬挂吊车和电动葫芦在每一跨间每条运行线路上考虑的台数,是按设计单位的使用经验确定的。
3.2.7梁柱连接一般采用刚性连接和较接连接。并刚性连接的弯矩转角关系较为复杂,它随连接形式、构造细节的不同而异。进行结构设计时,这种连接形式的实验数据或设计资料必须足以提供较为准确的夸矩转角关系。
3.2.8本条对框架结构的内力分析方法作出了具体规定,即所有框架结构(不论有无支撑结构)均可采用一阶弹性分析法计算框架杆件的内力,但对于框架结构则推荐采用二阶弹性分析法确定杆件内力,以提高计算的精确度。当采用二阶弹性分析时,为配合计算的精度,不论是精确计算或近似计算,亦不论有无支撑结构,均应考虑结构和构件的各种缺陷(如柱子的初倾斜、初偏心和残余应力等)对内力的影响。其影响程度可通过在框架每层柱的柱顶作用有附加的假想水平力(概念荷载)Hni来综合体现,见图1。
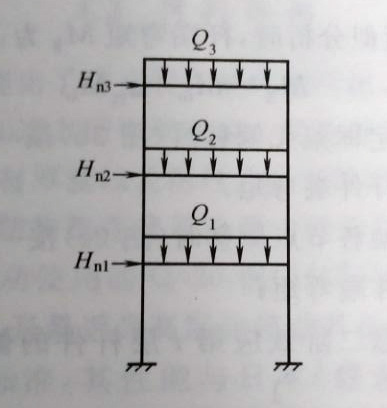
图1假想水平力Hni
研究表明,框架层数越多,构件缺陷的影响越小,且每层柱数的影响亦不大。通过与国外规范的比较分析,并考虑钢材强度的影响,本规范提出了Hni值的计算公式(3.2.8-1)。
至于柱子的计算长度则应根据不同类型的框架和内力分析方法,以及支撑结构的抗侧移刚度按本规范第5.3.3条的规定计算确定。
本条对无支棵纯框架在考虑侧移对内力的响采用二除弹性分析时,提出了框架杆件端弯矩MII的近似计算方法。
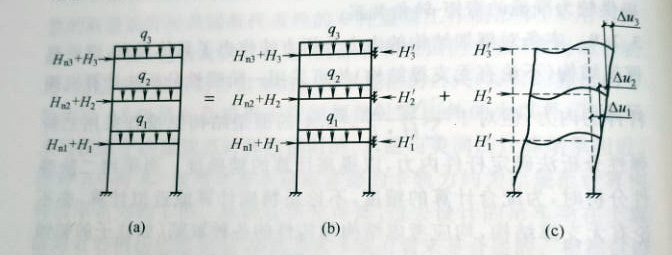
图2无支撑纯框架的一阶弹性分析
当采用一阶分析时(图2),框架杆件端弯矩M1为:
MI=MIb+MIs
当采用二阶近似分析时,杆端弯矩MII为:
MII=MIb+α2iMIs
式中MIb一假定框架无侧移时(图2b)按一阶弹性分析求得的各杆件端弯矩;
MIs一框架各节点侧移时(图2c)按一阶弹性分析求得的杆件端弯矩;
α2i一考虑二阶效应第i层杆件的侧移弯矩增大系数,
α2i=1/1-∑N?△u/∑H?h
其中∑H系指产生层间侧移△u的所计算是以上各层的水平荷载之和,不包括支座位移利度的作用。
上述二阶弹性分析的近似计算法与国外的规定基本相西安建筑科技大学陈绍蕃教授提出,湖南大学舒兴平教授以求秀1~3层无支撑纯框架为例,用二阶弹性分析精确法进行验证,结果表明:
1、此近似法不仅可用于二阶弯矩的计算,还可用于二阶轴力及剪力的计算。
2、在式(3.2.8-3)中,当∑N?△u/∑H?h≤0.25时,该近似法精确度较高,弯矩的误差不大于7%;而当∑N?△u/∑H?h>0.25(即α2i>1.33)时,误差较大,应增加框架结构的侧向刚度,使α2i≤1.33。
另外,当∑N?△u/∑H?h≤0.1 时,说明框架结构的抗侧移刚度较大,可忽略侧移对内力分析的影响,故可采用一阶分析法来计算框架内力,当然也就不再考虑假想水平力Hni,为判别时计算方便,式中△u可用层间侧移容许值[△u]来代替。
|
